numerical grid generation

A six-block quasi-isometric grid around a two-component Boeing airfoil given by a single mapping from the reference domain that is patched from six geodesic qnadrangles. The block boundaries are drawn red, the internal grid is black.

Detail of the grid.

Grid generation has been around since the dawn of the computational modeling. It is well known that the quality of the computational grid can significantly affect the convergence of the numerical scheme, as well as the final results. Grid generation "by hand" is very expensive in terms or man-hours. For complex domains it can take larger part of the total work. This is why automatic grid genereation has been a long-standing goal in industry and science.

The oldest numerical grid generation techniques are based upon the solution of elliptic PDE's. Typically, a Poission-type equation is solved given the boundary grid distribution to generate interior nodal points. The solution domain is often topologically equivalent to a cube in 3D and a square in 2D. One of drawbacks of these methods is that the mapping (usually a conformal mapping of a square onto the curvilinear domain) can have singularities in the corners of the domain. This creates two types of difficulties:

• The corner cells are not parallelograms
• When the grid in the square is refined uniformly, the grid in the domain becomes quite non-uniform, e.g., the corner cells are too large or too small.

These problems can be solved by changing the "prototype" domain from a square to a geodesic quadrangle on a surface of constant curvature. These are quadrangles that live on surface of a constant curvature (e.g., a sphere or a negative-curvature surface), and have the sides that are geodesics, the shortest paths between two points in the given metric. For example, on a plane the geodesics are straight lines and on sphere the geodesics are the great circles (such as the equator).

The geodesic quadrangle P is generated in such a way that it has same angles as the physical domain D, and a conformal mapping between the two is found. Therefore whatever grid we specify in P, will conformally be mapped into D.

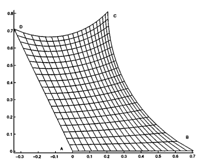
A prototype quadrangle on a surface of negative curvature.

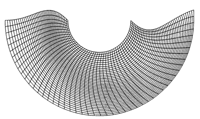
A target domain with negative angle defect.

For example, we can use this propery for the purpose of grid adaptation, as shown below using circle and a channel with wavy wall as examples (clickable).

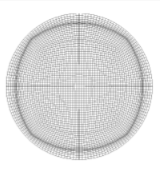
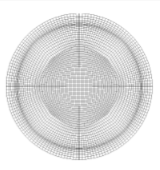
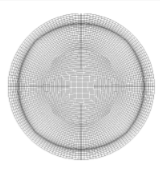
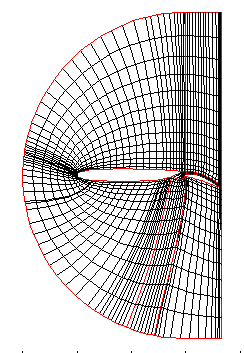
The algorithm that we have developed is extendable to multi-block grids, as shown in the figures above (circles) and on the right (multi-part wing). The grid around the two-part Boeing airfoil consists of 6 connected blocks, yet it is given by a single mapping. In this case, the prototype domain consists of six different quadrangles on six different surfaces of six different constant curvatures, all "glued" together. Note that our approach guarantees the existence and uniqueness of such a mapping. This means that you cannot get two solutions to the meshing problem for one set of specified parameters.

relevant publications

• GA Chumakov, SG Chumakov, A Method for the 2-D Quasi-Isometric Regular Grid Generation, J. Comput. Phys., 143 1-28 (1998)
• GA Chumakov, SG Chumakov, SiGMA &mdash a 2-D Quasi-Isometric Grid Generator, CRC Handbook of Grid Generation , CRC Press, A-53 (1999)